El código se puede encontrar en, se puede interactuar haciendo click y oprimiendo las teclas X, P y W para ver cómo los cambios de palabras alteran la forma de codificación de los qhipus:

https://openprocessing.org/sketch/1966565

video

September 5 - 14 Leaky Archive residency week I

Part I - On Quipus and graph systems

Contemporary translations and archaeological studies of quipus are often full of interpretations that imply that the coding and numbering systems used today are related to the complex representational systems hidden in the Inca quipus. However, despite the enormous historiographical advances in the decoding of certain functionalities of the textile pieces, there are still many obscure places in the enormous complexity of the settings and forms of these textiles. Such passages can be fundamental pieces for the approach of an alternate history of codification, that is, a rupture that can lead us to a decolonial computation. The three-dimensional representation, the corporeality and gesturality of the knots, the symbolism of the textile fibers (some even coming from animals, with enormous cosmogonic values), the plurality of connections and the spatialization of the representation are characteristics that, beyond possible comparison with contemporary mathematics, show the deep implication that the fact of including, as a constituent part of the system, the symbolic character of its own cultural understanding of the cosmos, can have for a representation of the world - and a codification of the world.3

To begin to unpack the implications of a spatial system of representation and coding such as the Quipus, it is useful to think about contemporary graph systems. Graphs are abstract structures formed by nodes or vertices, they are considered connected when they fulfill a certain property or relation. Often the nodes are represented as points in the plane and the connections by segments or arcs of curves joining them. The origin of graph theory goes back to the 18th century with the Königsberg bridge problem, which consisted of finding a path across the seven bridges of the Pregel river in the city of Königsberg, now Kaliningrad, in such a way that all the bridges were crossed by passing only once over each one of them. Leonhard Euler's work on the problem entitled Solutio problematis ad geometriam situs pertinentis (The solution of a problem concerning the geometry of position) in 17365 is considered the first result of graph theory. It is also considered one of the first topological results in geometry (which does not depend on any measure). There is a deep relationship between graph theory and topology.

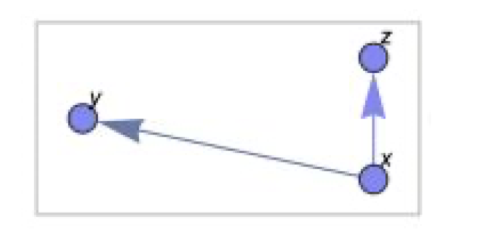
Figure 1.graph model consisting of three connecting nodes, on the right graphical representation of an Inca quipu system.

We can imagine a graph in which the nodes correspond to proteins and their relationships with other compounds, another in which the nodes are associated with Internet servers and the edges are the direct links between them, or a third in which the vertices are points on the plane or in space whose coordinates have been captured by a laser cannon, joined by edges that constitute a mesh that allows them to be represented. It is the abstract versatility of graphs as a structure that explains the wide range of applications in which they are currently used.

Strictly speaking, for a mathematician, a quipu is neither a knot (a closed loop in space) nor a link, a collection of non-intersecting knots in space. But they are links in a generalized sense in that they would be links if the ends of the individual ropes were connected. It is not so much the topology of quipu which is of interest for researchers but the information content which is encoded topologically. Because only three different type of knots appear in Inka style data (simple knots, figure eight knots and long knots) (whose topology is well understood), these entities could be replaced by symbols like L4,S,E standing for a long knot with 4 turns, a single knot or a figure eight knot. A quipu can be described as a graph on which scalar and vector data are attached. The scalar data assign to a node the knot type or the attachment type, if the node is branching off there. The vector data which describe the connecting strings are determined by ply and spin direction, attachment type, color and the material of the knot. For a computer scientist a quipu is an example of a graph database.

https://people.math.harvard.edu/~knill/history/khipu/khipu.pdf Oliver Knill, the Quipu enigma.

Many graphs are geometric in nature, such as transport networks, the meshes used for the graphical representation of objects, or the proximity graphs that allow point clouds to be analyzed, but there are many more, such as molecular structures, proteins, some of whose properties are studied in terms of rigidity, folding and coupling, whose formulation is clearly geometric. Graph theory is one of the fields of interaction between computational biology and computational geometry.

An interesting example of the use of graphs is provided by the recent studies of Stephen Wolfram. For the scientist, graphs constitute an alternative model for the representation and analysis of topics related to contemporary physics. Wolfram's theory6 starts from a basic substitution formula that unveils a fundamental principle. A list of simple instructions can configure a complex system if the system develops over time.

5 ​Euler, L. (1736). ​Solutio problematis ad geometriam situs pertinentis»​.. 128-140. 6

https://writings.stephenwolfram.com/2020/04/finally-we-may-have-a-path-to-the-fundamental-theory-of-physics-and-its-beautiful

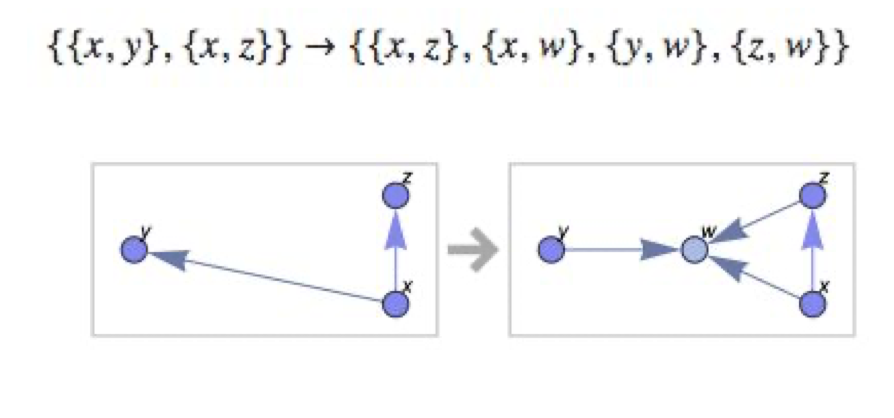
Figure 2. substitution formula and evolution sequence of networks

The graph above is a substitution model that reconfigures the network of nodes by adding one component and two additional connections. Wolfram's approach has roots in the theory of automata, mathematical models that build from simple rules to create dynamic systems that evolve in steps over time (Figure 3). The theory of cellular automata begins with its precursor John von Neumann in the late 1940s with his book Theory of Self-reproducing Automata, where he proposes the possibility of developing a machine with the ability to build from itself other machines (self-reproducing).

Figure 3. Cellular automaton, at the bottom the rule on the basis of which the complex system evolved. Rule 30.

Following the idea that shapes the system in the figure above, graph substitution algorithms can generate intricate structures and thus complex and random behavior. The notion of randomness is particularly important in such systems. Think of organic structures: what set of processes over time had to happen for a compound to develop in X or Y ways? Let us focus on three mechanisms of randomness7 that are involved in the development of the compound. The first corresponds to the randomness of the environment, the set of foreign conditions that will influence the changes in the compound. The second is the randomness around the initial conditions that led the compound to originate, i.e. the set of initial conditions of the environment and the context in which it was formed. The third condition, much less explored than the previous two, is particularly important. The intrinsic randomness generated in the development of the compound.

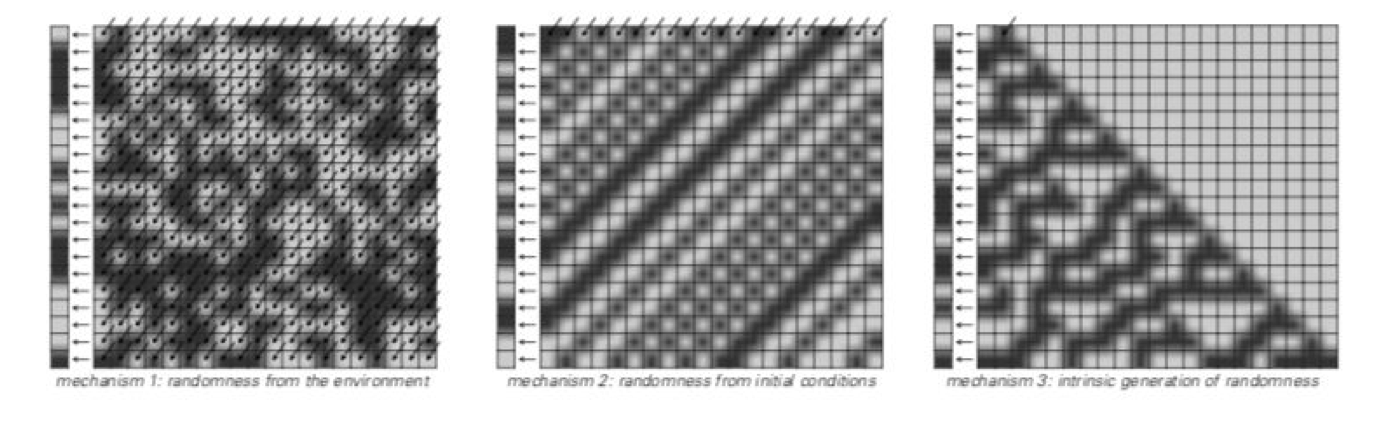
Figure 4. Mechanisms 1, 2 and 3 of randomisation

An important implication of this last randomness system dictates that it is possible that conditions 1 and 2 (the commonly explored ones) are just as relevant as condition 3 in the development of an organic system, and that a computational or algorithmic logic can be used to understand the evolution of organic systems. Let us return to the graph representation to see how several simple rule systems can evolve into highly complex forms 8.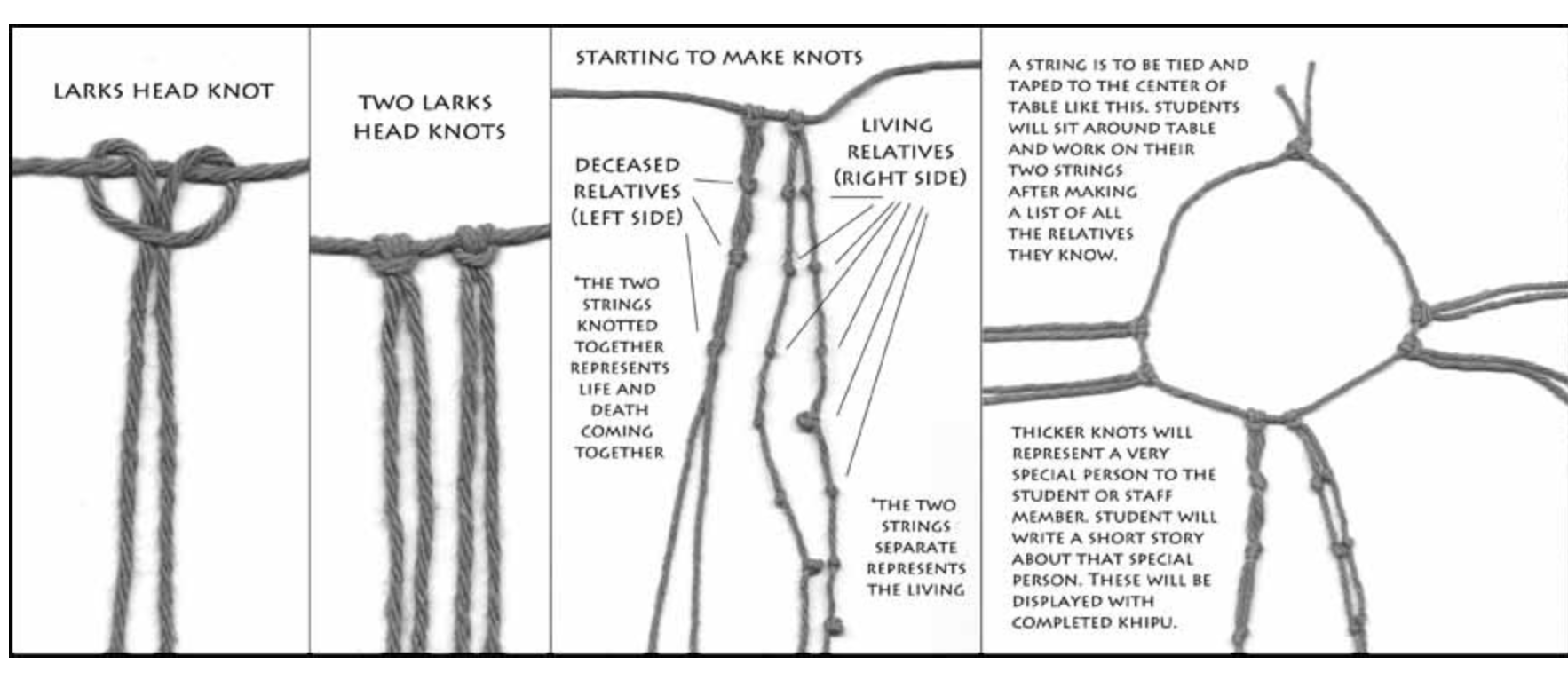

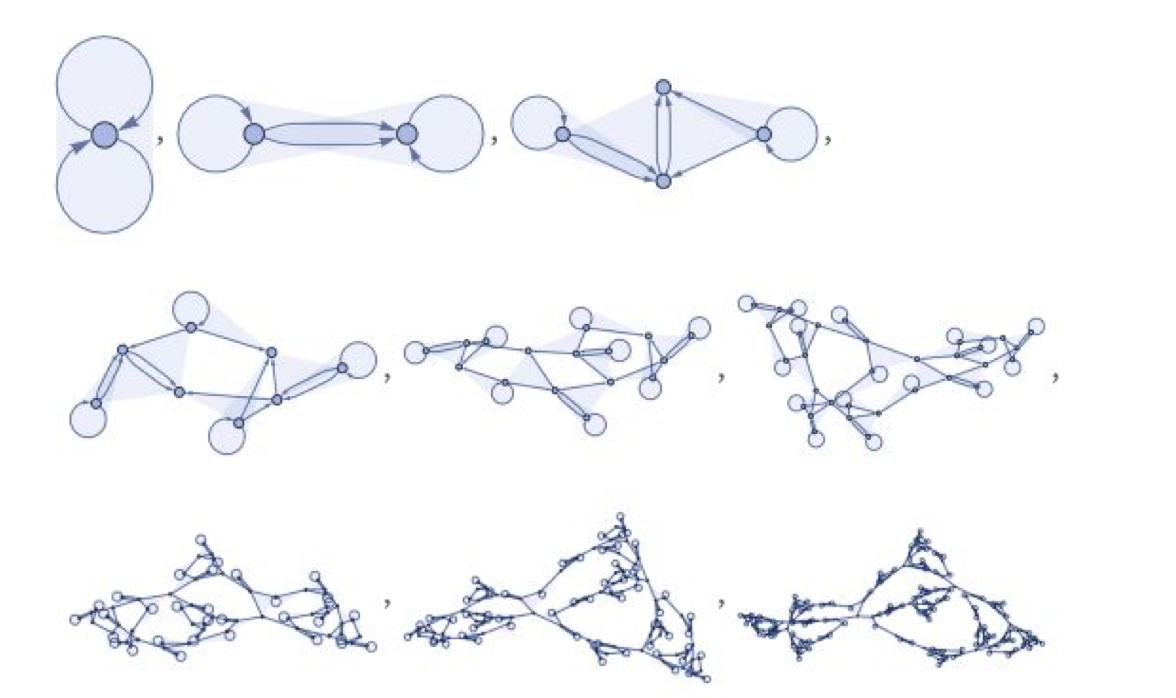
Figure 5. evolution of a system based on substitution with simple rules | different quipu nodes and structures

7 Wolfram, Stephen: A new kind of science. 2003 8

https://writings.stephenwolfram.com/2020/04/finally-we-may-have-a-path-to-the-fundamental-theory-of-physics-and-its-beautiful /

Altering the initial conditions implies a large chain of structural possibilities. A set of simple rules is capable of becoming highly complex systems on its own.

Let us consider a particular example: Soil. According to agrology, soil is equal to the function of (Climate, organisms, sediment strata and material from which soil is generated over time). This process constitutes Edaphogenesis9 , the formation of new soil.

S = f ( CL + O + MP + R + T)

It is in principle impossible to think that a particular simple sequence could explain such an intricate system, indeed, it could be argued that such a system need not operate under the constraint that its behavior is predictable or understandable. Such an example could have used a huge set of processes and rules that would not interlock with each other.

What this means is that a large number of components of any kind can be used. However, in sciences such as biology, the presence of systems with many separate parts can lead to a certain quite analogous complexity, similar to having many physical objects of different types put together. But the most dramatic examples of complexity tend to occur in individual parts of systems, and often involve patterns or structures that look remarkably like those in physics.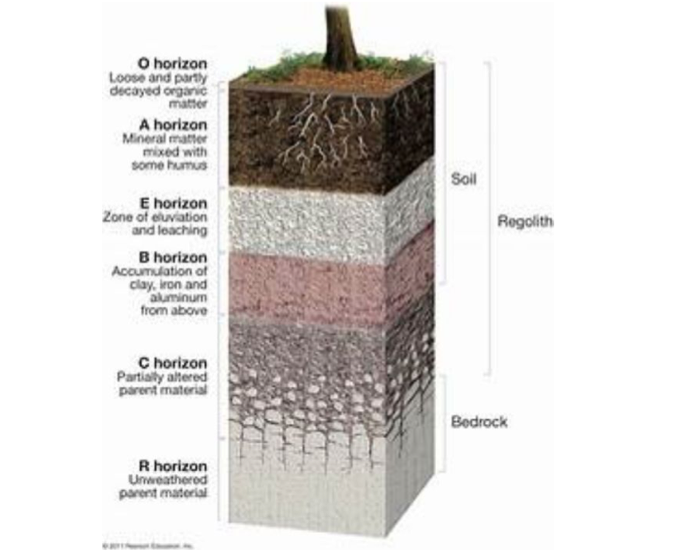

Figure 7. Soil profile with horizon classification.

9 Cortes, Abdon. Geografía de los suelos de Colombia. 1996.

If one begins to analyze specific parts of the elements that make up a metastable system such as the soil, one finds structures that begin to denote patterns and forms that show the potential for development based on concrete sequences. The soil profile is the X-ray that records the history of the natural evolutionary process and the anthropic phenomena that changed its course at a given moment of edaphogenesis. Soil horizons seem to denote a high and intricate set of initial relationships for the shaping of the system. However, when we stop to look at the processes of parental rock formation (which form, specifically, Horizon C of the profile) we can find that a sequence of rules such as the automaton 110 can show how, from simple initial rules, the process of positioning of the parental material that forms the soil in this stratum can be described.

Figure 8. Rule 110 automaton (left). C-horizon of the ground in profile representation

This conjecture also has implications for the way evolution has been understood around natural selection and competition. The basic notion that organisms tend to evolve through natural selection to achieve maximum fitness has certainly been useful in the past for providing a general framework for understanding the historical progression of species and for providing specific explanations for a number of fairly simple properties of particular species. However, it is a problematic feature that falls short in many ways.

"But in current thinking about biology, the notion has tended to be taken to the extreme, so that especially among those who are not in daily contact with detailed data on biological systems, it has been assumed that essentially every feature of every organism can be explained on the basis of it somehow maximizing the fitness of the organism.

It is certainly recognised that some aspects of today's organisms are indeed remnants of earlier stages in biological evolution. And there is also a growing awareness that the actual process of growth and development within an individual organism can make it easier or more difficult for particular types of structures to occur. But beyond this, there is a surprisingly universal conviction that any significant property one sees in any organism must be there because, in essence, it has a purpose in maximizing the fitness of the organism." 10

In this sense, what we understand as the solutions of biological organisms to problems in their development are not optimal solutions. Rather, they are characteristics in which complexity is hybridized from initial conditions, the relationship of the organism's system networks with the surrounding networks and systems, and the emergent solutions were sufficient not to cause fatal problems for the organism.

The structuring and encryption of information from the perspective of the quipus allows, at a first glance, to glimpse a system where encryption, narrative and symbolic weaving are united towards a representation of a cosmogony where limits between disciplines and models of understanding do not have the limitations of the frontiers of current systems.

September 5 - 14 Leaky Archive residency week I

Part I - On Quipus and graph systems

Contemporary translations and archaeological studies of quipus are often full of interpretations that imply that the coding and numbering systems used today are related to the complex representational systems hidden in the Inca quipus. However, despite the enormous historiographical advances in the decoding of certain functionalities of the textile pieces, there are still many obscure places in the enormous complexity of the settings and forms of these textiles. Such passages can be fundamental pieces for the approach of an alternate history of codification, that is, a rupture that can lead us to a decolonial computation. The three-dimensional representation, the corporeality and gesturality of the knots, the symbolism of the textile fibers (some even coming from animals, with enormous cosmogonic values), the plurality of connections and the spatialization of the representation are characteristics that, beyond possible comparison with contemporary mathematics, show the deep implication that the fact of including, as a constituent part of the system, the symbolic character of its own cultural understanding of the cosmos, can have for a representation of the world - and a codification of the world.3

To begin to unpack the implications of a spatial system of representation and coding such as the Quipus, it is useful to think about contemporary graph systems. Graphs are abstract structures formed by nodes or vertices, they are considered connected when they fulfill a certain property or relation. Often the nodes are represented as points in the plane and the connections by segments or arcs of curves joining them. The origin of graph theory goes back to the 18th century with the Königsberg bridge problem, which consisted of finding a path across the seven bridges of the Pregel river in the city of Königsberg, now Kaliningrad, in such a way that all the bridges were crossed by passing only once over each one of them. Leonhard Euler's work on the problem entitled Solutio problematis ad geometriam situs pertinentis (The solution of a problem concerning the geometry of position) in 17365 is considered the first result of graph theory. It is also considered one of the first topological results in geometry (which does not depend on any measure). There is a deep relationship between graph theory and topology.

Figure 1.graph model consisting of three connecting nodes, on the right graphical representation of an Inca quipu system.

We can imagine a graph in which the nodes correspond to proteins and their relationships with other compounds, another in which the nodes are associated with Internet servers and the edges are the direct links between them, or a third in which the vertices are points on the plane or in space whose coordinates have been captured by a laser cannon, joined by edges that constitute a mesh that allows them to be represented. It is the abstract versatility of graphs as a structure that explains the wide range of applications in which they are currently used.

Strictly speaking, for a mathematician, a quipu is neither a knot (a closed loop in space) nor a link, a collection of non-intersecting knots in space. But they are links in a generalized sense in that they would be links if the ends of the individual ropes were connected. It is not so much the topology of quipu which is of interest for researchers but the information content which is encoded topologically. Because only three different type of knots appear in Inka style data (simple knots, figure eight knots and long knots) (whose topology is well understood), these entities could be replaced by symbols like L4,S,E standing for a long knot with 4 turns, a single knot or a figure eight knot. A quipu can be described as a graph on which scalar and vector data are attached. The scalar data assign to a node the knot type or the attachment type, if the node is branching off there. The vector data which describe the connecting strings are determined by ply and spin direction, attachment type, color and the material of the knot. For a computer scientist a quipu is an example of a graph database.

https://people.math.harvard.edu/~knill/history/khipu/khipu.pdf Oliver Knill, the Quipu enigma.

Many graphs are geometric in nature, such as transport networks, the meshes used for the graphical representation of objects, or the proximity graphs that allow point clouds to be analyzed, but there are many more, such as molecular structures, proteins, some of whose properties are studied in terms of rigidity, folding and coupling, whose formulation is clearly geometric. Graph theory is one of the fields of interaction between computational biology and computational geometry.

An interesting example of the use of graphs is provided by the recent studies of Stephen Wolfram. For the scientist, graphs constitute an alternative model for the representation and analysis of topics related to contemporary physics. Wolfram's theory6 starts from a basic substitution formula that unveils a fundamental principle. A list of simple instructions can configure a complex system if the system develops over time.

5 ​Euler, L. (1736). ​Solutio problematis ad geometriam situs pertinentis»​.. 128-140. 6

https://writings.stephenwolfram.com/2020/04/finally-we-may-have-a-path-to-the-fundamental-theory-of-physics-and-its-beautiful

Figure 2. substitution formula and evolution sequence of networks

The graph above is a substitution model that reconfigures the network of nodes by adding one component and two additional connections. Wolfram's approach has roots in the theory of automata, mathematical models that build from simple rules to create dynamic systems that evolve in steps over time (Figure 3). The theory of cellular automata begins with its precursor John von Neumann in the late 1940s with his book Theory of Self-reproducing Automata, where he proposes the possibility of developing a machine with the ability to build from itself other machines (self-reproducing).

Figure 3. Cellular automaton, at the bottom the rule on the basis of which the complex system evolved. Rule 30.

Following the idea that shapes the system in the figure above, graph substitution algorithms can generate intricate structures and thus complex and random behavior. The notion of randomness is particularly important in such systems. Think of organic structures: what set of processes over time had to happen for a compound to develop in X or Y ways? Let us focus on three mechanisms of randomness7 that are involved in the development of the compound. The first corresponds to the randomness of the environment, the set of foreign conditions that will influence the changes in the compound. The second is the randomness around the initial conditions that led the compound to originate, i.e. the set of initial conditions of the environment and the context in which it was formed. The third condition, much less explored than the previous two, is particularly important. The intrinsic randomness generated in the development of the compound.

Figure 4. Mechanisms 1, 2 and 3 of randomisation

An important implication of this last randomness system dictates that it is possible that conditions 1 and 2 (the commonly explored ones) are just as relevant as condition 3 in the development of an organic system, and that a computational or algorithmic logic can be used to understand the evolution of organic systems. Let us return to the graph representation to see how several simple rule systems can evolve into highly complex forms 8.

Figure 5. evolution of a system based on substitution with simple rules | different quipu nodes and structures

7 Wolfram, Stephen: A new kind of science. 2003 8

https://writings.stephenwolfram.com/2020/04/finally-we-may-have-a-path-to-the-fundamental-theory-of-physics-and-its-beautiful /

Altering the initial conditions implies a large chain of structural possibilities. A set of simple rules is capable of becoming highly complex systems on its own.

Let us consider a particular example: Soil. According to agrology, soil is equal to the function of (Climate, organisms, sediment strata and material from which soil is generated over time). This process constitutes Edaphogenesis9 , the formation of new soil.

S = f ( CL + O + MP + R + T)

It is in principle impossible to think that a particular simple sequence could explain such an intricate system, indeed, it could be argued that such a system need not operate under the constraint that its behavior is predictable or understandable. Such an example could have used a huge set of processes and rules that would not interlock with each other.

What this means is that a large number of components of any kind can be used. However, in sciences such as biology, the presence of systems with many separate parts can lead to a certain quite analogous complexity, similar to having many physical objects of different types put together. But the most dramatic examples of complexity tend to occur in individual parts of systems, and often involve patterns or structures that look remarkably like those in physics.

Figure 7. Soil profile with horizon classification.

9 Cortes, Abdon. Geografía de los suelos de Colombia. 1996.

If one begins to analyze specific parts of the elements that make up a metastable system such as the soil, one finds structures that begin to denote patterns and forms that show the potential for development based on concrete sequences. The soil profile is the X-ray that records the history of the natural evolutionary process and the anthropic phenomena that changed its course at a given moment of edaphogenesis. Soil horizons seem to denote a high and intricate set of initial relationships for the shaping of the system. However, when we stop to look at the processes of parental rock formation (which form, specifically, Horizon C of the profile) we can find that a sequence of rules such as the automaton 110 can show how, from simple initial rules, the process of positioning of the parental material that forms the soil in this stratum can be described.

Figure 8. Rule 110 automaton (left). C-horizon of the ground in profile representation

This conjecture also has implications for the way evolution has been understood around natural selection and competition. The basic notion that organisms tend to evolve through natural selection to achieve maximum fitness has certainly been useful in the past for providing a general framework for understanding the historical progression of species and for providing specific explanations for a number of fairly simple properties of particular species. However, it is a problematic feature that falls short in many ways.

"But in current thinking about biology, the notion has tended to be taken to the extreme, so that especially among those who are not in daily contact with detailed data on biological systems, it has been assumed that essentially every feature of every organism can be explained on the basis of it somehow maximizing the fitness of the organism.

It is certainly recognised that some aspects of today's organisms are indeed remnants of earlier stages in biological evolution. And there is also a growing awareness that the actual process of growth and development within an individual organism can make it easier or more difficult for particular types of structures to occur. But beyond this, there is a surprisingly universal conviction that any significant property one sees in any organism must be there because, in essence, it has a purpose in maximizing the fitness of the organism." 10

In this sense, what we understand as the solutions of biological organisms to problems in their development are not optimal solutions. Rather, they are characteristics in which complexity is hybridized from initial conditions, the relationship of the organism's system networks with the surrounding networks and systems, and the emergent solutions were sufficient not to cause fatal problems for the organism.

The structuring and encryption of information from the perspective of the quipus allows, at a first glance, to glimpse a system where encryption, narrative and symbolic weaving are united towards a representation of a cosmogony where limits between disciplines and models of understanding do not have the limitations of the frontiers of current systems.

https://docplayer.es/112882814-Umberto-roncoroni-editor-lima.html Umberto Ronroroni , medios digitales e identidad cultural

https://www.researchgate.net/publication/342620622_Pensamiento_computacional_Alfabetizacion_digital_sin_computadoras

https://ars.electronica.art/outofthebox/de/khipu-2/

https://proyectokhipu.wordpress.com/2021/09/19/conferencias/ — mas informacion sobre el proyecto

Los inca khipu son dispositivos textiles para registrar información, hechos de hilos de algodón o fibra de camélidos que almacenan datos codificados como nudos. Esta pieza es una computadora textil de código abierto basada en la fabricación de khipu astronómico, cuyos cables fueron hilados a mano con lana de alpaca y alambre de cobre. Funciona como una antena para campos electromagnéticos que está conectada a un circuito amplificador. Los datos codificados en él corresponden a: una clasificación espectral de las estrellas en la constelación de Boötes; un calendario lunar, un eclipse solar; dos terremotos, y la posición elíptica del sol y la luna en el momento de nuestros nacimientos.

Este proyecto es una interpretación sonora y artística de la tecnología, la sabiduría y la historia de nuestros antepasados, destinada a expresar cómo el universo se rige por proporciones numéricas armoniosas. Lo que estamos escuchando ahora es, pues, la amplificación del espacio inaudible, las voces de los espectros que visitan el vacío, una partitura celestial, la música de las esferas: la voz del silencio.

https://www.youtube.com/watch?v=KQn5esRLQiM de Patricia Cadavid y Enrique Tomas

https://www.youtube.com/watch?v=2_YLzO-XFcg Proyecto Khipu de Cecilia Vicuña

—---------

https://www.youtube.com/watch?v=1-UNiy1NHEs&t=2240s — Computación decolonial, panel con varias ponencias sobre investigaciones y recursos para plantear las implicaciones de computación prehispánica

https://www.youtube.com/watch?v=q1Hh2utr-vY —-- Sobre las implicaciones de los cambios de codificación en la divulgación histórica

—--------